(per iscrizioni A.A. 2022/23) 
Scomposizione in fattori: che cos’è e come si fa
Se sei uno studente alle prese con l’esame di matematica presso l’Università online Niccolò Cusano di Brescia, saprai sicuramente che un concetto fondamentale di questa materia è la scomposizione in fattori.
Nel corso di questa guida cercheremo di spiegare in maniera chiara di cosa si tratta, dando una definizione di scomposizione in fattori e cercando di capire come si effettua.
Iniziamo dunque dal suo significato.
Scomposizione in fattori: che cos’è?
Prima di tutto è necessario dare una definizione al concetto di scomposizione in fattori. In algebra infatti una delle operazioni più importanti è la cosiddetta scomposizione di un polinomio in fattori. Si tratta di quell’operazione algebrica tramite la quale scriviamo un polinomio sotto forma di prodotto tra due o più fattori di grado inferiore, detta anche fattorizzazione di un polinomio.
I fattori di grado inferiore possono essere singoli monomi o polinomi in parentesi. Esistono inoltre polinomi che non possono essere espressi come prodotto di fattori di grado inferiore. E’ il caso dei polinomi irriducibili.
Come scomporre un numero in fattori primi
Adesso che abbiamo gettato le basi per comprendere la scomposizione in fattori, vediamo prima come si effettua la scomposizione di un numero in fattori primi per poi passare alla scomposizione di polinomi in fattori primi.
La scomposizione in fattori primi, detta anche fattorizzazione in numeri primi, è un procedimento algebrico che consiste nel riscrivere un numero naturale come prodotto di numeri primi.
Numeri naturali e numeri primi
Cosa è un numero primo? Un numero primo è un numero naturale maggiore di 1 che può essere diviso solamente per 1 o per se stesso.
I primi dieci numeri naturali sono: 2, 3, 5, 7, 11, 13, 17, 19, 23 e 29.
Cosa è un numero naturale? I numeri naturali, indicati in maniera generica con N,
sono tutti i numeri, quindi 0, 1, 2, 3, 4, 5…e si ottengono aggiungendo ogni volta un’unità a partire da 0.
I numeri naturali sono infiniti e sono numeri interi non negativi.
Criteri di divisibilità
Tornando alla scomposizione in fattori primi, ora che sappiamo la differenza tra numeri primi e numeri naturali, la prima cosa da imparare sono i criteri di divisibilità.
Negli esercizi di algebra, i criteri che ritroviamo più frequentemente sono:
- criterio di divisibilità per 2
- criterio di divisibilità per 3
- criterio di divisibilità per 5
A) criterio di divisibilità per 2 si applica quando un numero naturale è divisibile per 2, ovvero quando la cifra dell’unità è 0 – 2 – 4 – 6 – 8 ed è quindi un numero pari.
B) criterio di divisibilità per 3 si applica quando un numero naturale è divisibile per 3, ovvero quando la somma delle sue cifre è un multiplo di 3.
C) criterio di divisibilità per 5 si applica quando un numero naturale è divisibile per 5, ovvero quando la cifra dell’unità è 0 o 5.
Esempi pratici di scomposizione di un numero in fattori primi
Immaginiamo di voler scomporre un numero naturale.
Se si tratta di un numero primo, il procedimento è molto breve perché la scomposizione è data dal numero stesso.
Se si tratta di un numero non primo, allora applichiamo il procedimento e i criteri di divisibilità descritti poco fa.
Vediamo quindi qual è il metodo per scomporre in fattori primi un numero non primo, come ad esempio 180.
Il numero naturale non primo 180 che ha lo 0 come unità, è un numero pari e la somma delle sue cifre è 9.
Questo vuol dire che si possono applicare tutti e tre i criteri di divisibilità, per 2 – 3 e 5.
Applichiamo il criterio di divisibilità per 5.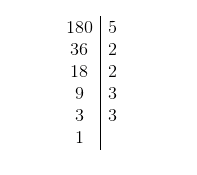
Cosa notiamo? Nella colonna di sinistra riportiamo i risultati della divisione e nella colonna di destra i numeri primi con cui dividiamo i numeri naturali della colonna di sinistra, fino ad ottenere come ultimo numero a sinistra il numero naturale primo 1.
A questo punto la scomposizione in fattori è terminata e possiamo scrivere il numero 180 come prodotto di numeri primi sotto forma di potenza, ovvero:
180 = 22 x 33 x 5
Per conoscere i numeri primi è stata creata per convenienza l’apposita tabella dei numeri primi.
Perché si utilizza la scomposizione in fattori primi
Il metodo della scomposizione in fattori primi è usato in matematica per:
- trovare i divisori di un numero
- verificare se due numeri sono divisibili tra loro senza eseguire la divisione
- calcolare il massimo comune divisore o il minimo comune multiplo
- ridurre una frazione ai minimi termini
Come scomporre un polinomio in fattori primi
Vista la scomposizione in fattori primi, vediamo adesso la scomposizione di polinomi in fattori primi, ripartendo da due concetti citati all’inizio della nostra guida, ovvero monomi e polinomi.
Differenza tra monomi e polinomi
Vediamo dunque cosa significano questi due termini:
- monomi
- polinomi
Il monomio è un’espressione algebrica che consiste nel prodotto di fattori qualsiasi, sia numerici che letterali con esponente a numero naturale.
Facciamo un esempio: 4x2
4 è il fattore numerico definito anche coefficiente, mentre x2 è il fattore letterale.
Nel monomio la parte numerica può essere costituita da un numero qualsiasi che viene moltiplicato per la parte letterale, mentre nella parte letterale possono esserci solo moltiplicazioni.
Il polinomio è un qualsiasi monomio o la somma algebrica tra più monomi.
Facciamo un esempio: 5 – z + 2xy
Si tratta di un polinomio in quanto è formato dalla somma di monomi.
In base al numero di termini di cui si compone il polinomio possiamo avere:
binomi, ovvero polinomi formati da due monomi non simili
trinomi, ovvero polinomi formati da tre monomi non simili
quadrinomi, ovvero polinomi formati da quattro monomi non simili
e così via, dove per monomi simili intendiamo monomi che, ridotti in forma normale, hanno la stessa parte letterale.
Facciamo un esempio:
xy2z ; 3/2 xy2z
sono monomi simili in quanto la parte letterale è la stessa.
La scomposizione dei polinomi in fattori primi
Ora che abbiamo visto la differenza tra monomi e polinomi, cercheremo di spiegare la scomposizione dei polinomi in fattori primi, attraverso due metodi di raccoglimento:
- Raccoglimento totale a fattor comune
- Raccoglimento parziale a fattor comune
Il primo è molto più semplice da applicare rispetto al secondo.
Nei termini di un polinomio da scomporre, potrebbe esserci un fattore (numerico o letterale) comune a tutti i termini. In questo caso l’operazione di raccoglimento di questo fattore è detta raccoglimento totale.
Tecnicamente
“il risultato di un raccoglimento totale sarà la scomposizione del polinomio in un prodotto di un opportuno monomio e di un polinomio con lo stesso numero di elementi del polinomio di partenza”.
Facciamo un esempio di raccoglimento totale a fattor comune:
20x4y + 10x2y3 + 12x2y2+ 8x2
Cosa hanno in comune questi quattro termini?
I coefficienti sono divisibili tutti per 2;
le parti letterali hanno la lettera x all’interno con massimo esponente 2
Quindi i monomi sono tutti divisibili per 2x2
Pertanto il polinomio di partenza può essere così raccolto:
2x2 (10x2y + 5y3 + 6y2 + 4)
Siamo di fronte ad un raccoglimento totale.
Nel caso di un raccoglimento parziale, in cui i termini si separano in due parti, il risultato della scomposizione è il prodotto di due polinomi.
Facciamo un esempio di raccoglimento parziale a fattor comune:
12xy – 8x + 9zy – 6z
Separiamo i primi due termini 12xy – 8x da + 9zy – 6z
e raccogliamo 4x dai primi due e 3z dagli altri due.
Cosa otteniamo?
4x(3y – 2) +3z (3y – 2)
Vediamo che i polinomi ottenuti sono gli stessi, pertanto 12xy – 8x + 9zy – 6z = (4x + 3z) (3y – 2)
Ora che abbiamo rispolverato la mente su concetti e nozioni matematiche molto note, vogliamo giungere al termine della nostra guida ricordandoti che puoi chiedere sempre informazioni sui corsi di laurea attivi presso l’Università online Niccolò Cusano di Brescia attraverso il form che trovi qui di lato e che nello specifico “Istituzioni di matematica” è una delle materie previste dai nostri corsi di ingegneria. Se vuoi specializzarti in ingegneria biomedica a Brescia leggi come fare sul nostro blog.
